Septembre, I.; Meyer, J. S.; Solnyshkov, D. D.; Malpuech, G. Weyl singularities in polaritonic multiterminal Josephson junctions Phys. Rev. B 107, 165301 (2023) https://doi.org/10.1103/PhysRevB.107.165301
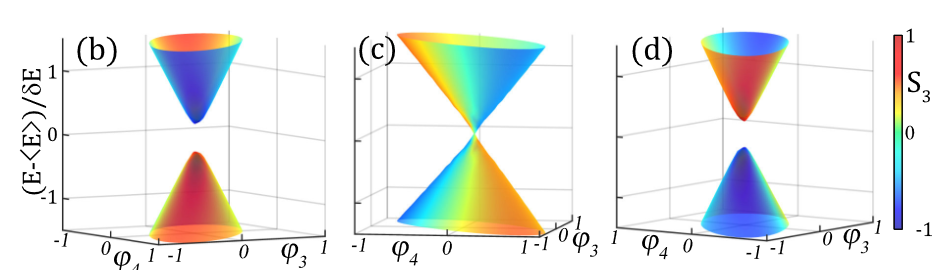
We study theoretically analog multiterminal Josephson junctions formed by gapped superfluids created upon resonant pumping of cavity exciton polaritons. We study the p-like bands of a five-terminal junction in the four-dimensional (4D) parameter space created by the superfluid phases acting as quasimomenta. We find 4/6 Weyl points in 3D subspaces with preserved/broken time-reversal symmetry. We link the real space topology (vortices) to the parameter space one (Weyl points). We derive an effective Hamiltonian encoding the creation, motion, and annihilation of Weyl nodes in 4D. Our work paves the way to the study of exotic topological phases in a platform allowing direct measurement of eigenstates and band topology.

