D. D. Solnyshkov, I. Septembre, K. Ndiaye, and G. Malpuech Analog of Foucault precession in two-dimensional quantum harmonic oscillators with Berry curvature Phys. Rev. B 108, 144306 https://doi.org/10.1103/PhysRevB.108.144306
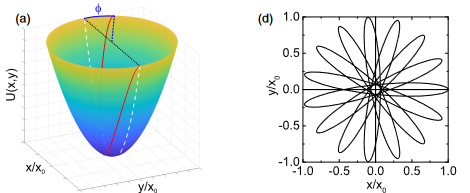
The geometric phase plays a key role both in the rotation of the Foucault pendulum and in the anomalous Hall effect (AHE), where an accelerated wave packet shows a transverse motion induced by the Berry curvature. Here, we show that the motion of quantum particles described by a spin-orbit-coupling Hamiltonian showing nonzero Berry curvature and placed in a two-dimensional harmonic-oscillator potential in real space exhibits Foucault precession. The plane of the oscillations rotates with time. The rotating pendulum configuration enhances the spatial deviation with respect to the AHE case, simplifying its observation and allowing high-precision measurements of the Berry curvature. We show how the nonadiabaticity and anharmonicity determine the maximal rotation angle and find the optimal conditions for the observations.

